数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。可透过程序语言所提供的数据类型、引用及其他操作加以实现。一个设计良好的数据结构，应该在尽可能使用较少的时间与空间资源的前提下，支持各种程序运行。透过将数据结构的具体实现封装隐藏于用户界面之后的方法，来让不同的应用程序能够安全地重用这些数据结构。

线性表

线性表(Linear List)简称表，是n(n≥0)个元素的有限序列。
其中：

  • 数据元素的个数n定义为表的长度 = list.length() （list.length() = 0，称为空表）
  • 将非空的线性表（n>=0）记作：（a[0]，a[1]，a[2]，…，a[n-1]）
  • 数据元素a[i]（0≤i≤n-1）只是个抽象符号，其具体含义在不同情况下可以不同

顺序表

顺序表是在计算机内存中以数组的形式保存的线性表，是指用一组地址连续的存储单元依次存储数据元素的线性结构。

链表

链表（Linked list）是不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)，单链表如图:

线性表应当给予以下的基本操作：搜索，删除、插入某个元素。下面，我们以双向链表实现一下。双向链表，顾名思义，就是数据本身具备了左边和右边的俩个指针。假如说双向链表的每个元素都是一个对象，那么每个对象都有一个关键字key，和俩个指针prev，next。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
LIST-SEARCH(L, k)   //L为链表头，k为所要查找的key
x = L.head
while x != NIL and x.key != k
    x = x.next
return x

LIST-INSERT(L, x)   //L为链表头，x为所要插入的元素(头插法)
x.next = L.head
if L.head != NIL
    L.head.prev = x
L.head = x
x.prev = NIL

LIST-DELETE(L, x)   //L为链表头，x指向所要删除的元素
if x.prev != NIL
    x.prev.next = x.next
else L.head = x.next
if x.next != NIL
    x.next.prev = x.prev

栈

栈(Stack)，由于数据只允许在一端进行操作，因而是一种后进先出(last-in, first-out, LIFO)策略。栈上的INSERT操作被称为压入(PUSH)，而无参数的DELETE操作被称为弹出(POP)。如图：

栈应当给予以下的基本操作：判断栈是否为空，入栈，出栈。以下我们会以数组实现基本操作。该数组具有一个属性S.top，指向最新插入的元素。栈中包括的元素S[0..S.top]，其中S[0]是栈底元素，S[S.top]是栈顶元素。当S.top=-1时，栈中不包括任何一个元素，即栈空(empty)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
STACK-EMPTY(S)  
if S.top == -1
    return TRUE
else return FALSE

STACK-PUSH(S, x)   //如果S.top超过了数组上限，称为上溢(overflow)
if(S.top == n)
    error "overflow"
S.top = S.top + 1
S.[S.top] = x

STACK-POP(S)    //如果S.top超过了数组下界，称为下溢(underflow)
if S.top == -1
    error "underflow"
else S.top = S.top - 1
     retun S[S.top + 1]

队列

队列(Queue)，只允许在后端（称为rear）进行插入操作，在前端（称为front）进行删除操作。因而是先进先出（FIFO, First-In-First-Out）的线性表。队列的INSERT操作被称为是入队(ENQUEUE)，DELETE操作被称为是出队(DEQUEUE)。和栈的POP操作一样，DEQUEUE操作也没有元素参数。如图：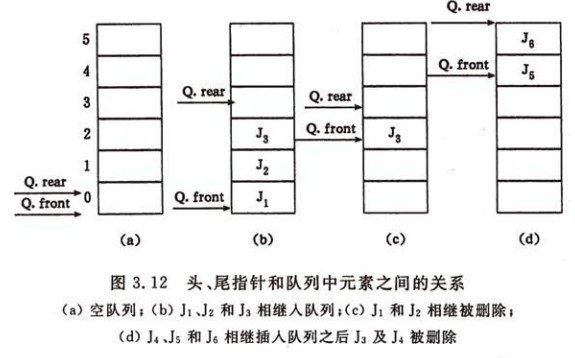

队列应当给予以下的基本操作：入队，出队。以下我们会以数组实现基本操作。该数组具有俩个属性Q.rear、Q.front，Q.rear指向最后一个元素，Q.front指向最新插入的元素。队列中包括的元素为Q[Q.rear..Q.front]。以下实现时，省略了上下溢检查。

1
2
3
4
5
6
7
8
9
10
11
12
QUEUE-ENQUEUE(Q, x)  
Q[Q.rear] = x
if Q.rear == Q.length
    Q.rear = 1
else Q.rear = Q.rear + 1

QUEUE-DEQUEUE(S)    
x = Q[Q.front]
if Q.front = Q.length
    Q.front = 1
else Q.front = Q.front + 1
return x

exercise :

  1. 给定一个单链表，如何判断是否为环
  2. 给定一个单链表，如果存在环，返回环的头指针，否则返回NULL
  3. 给定俩个单链表，如果有重合，返回重合的头指针，否则返回NULL
  4. 给定一个单链表，判断是否为回文链表
  5. 使用俩个栈实现一个队列
  6. 使用俩个队列实现一个栈